Posted 2024-03-03jdk

HashMap原理分析

未专门声明的情况，都是 1.8 的代码。

hash函数

确定桶的算法：

1	i = (n - 1) & hash

本质是为了将 hash 这个 int 通过取模，获得一个数组上的一个位置，这个获取需要均匀，等价于 i = hash % n。有点类似数据库分库分表的路由算法。

在 n 为 2 的 n 次方时，i = (n - 1) & hash 等价于 i = hash % n。并且性能更好，位运算比求余计算性能更好。

那么为什么在 n 为 2 的 N 次方时，i = (n - 1) & hash 等价于 i = hash % n？

hash % n，按照十进制算，就是 hash 除以 n 以后，余数就是取余的结果。如果按照二进制的除法考虑，n 是 2 的 N 次方，那么，比如 hash 为 11 即 1011，n 为 4 即 100，二进制数的除法 1011 除以 100，相当于把 1011 左边的两位抹去，最终得到 11，十进制值是 3，就是最终的余数。也就是说，如果除数的位数减一是 A，那么取余的结果就是被除数的最后 A 位。
那么如何得到最后 A 位呢？将 4 减 1 以后为 3，二进制是 11，用 11 和 1011 求余，刚好能得到最后 2 位的二进制值，也就是 11，十进制是 3。
https://zhuanlan.zhihu.com/p/458305988

那么这里解释了为什么 HashMap 的数组的容量必须是 2 的 n 次方，因为如果不是，就达不到均匀针对 hash 值取余的效果，无法将 k-v 对均匀的落到数组的每一个桶上。
资料： https://www.cnblogs.com/java1024/p/13488714.html

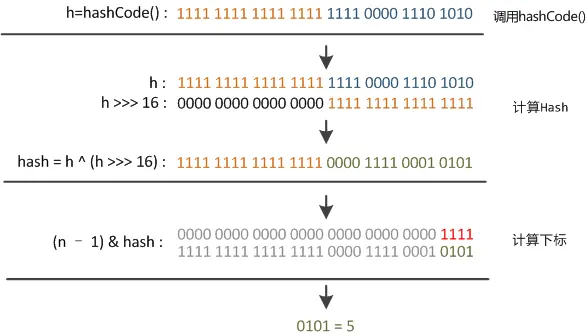
内部 hash 值计算：

static final int hash(Object key) {  
    int h;  
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);  
}

n 为偶数，那么 n - 1 的二进制表示全为 1，比如 n 为 8，n - 1 为 7，7 的二进制是三个 1。此时 i = (n - 1) & hash 实际是只针对 hash 的低位进行散列，这也会有问题。如果被 put 进来的 key 的 hashCode 的低位全是一致的，那么就会产生激烈的 hash 碰撞。

解决办法：将 hash 右移动 16 位，并与 hash 的原值做异或运算，得到的结果再做真正的散列。

为什么这么做？右移动 16 位以后，将 int 的高 16 位移动到了低 16 位，再和原 hash 做异或，可以让 hash 的高 16 位也参与到最终的散列中来，避免仅仅取低位进行散列造成的 hash 碰撞。

那么为什么用异或呢？异或的规则是「两个位相同时为 0，相异为 1」，根据高低位的不同情况：

高位	低位	异或结果
1	1	0
0	1	1
1	0	1
0	0	0
如果低位固定的情况，高位的变动能显著影响最终的结果，比如低位固定 1，高位位 1 和 0 的情况下，最终的结果不一样，那么在高位对低位执行异或以后，可以结合高位和低位产生一个更离散的 hash 值。避免了仅用 hashCode 的低位去做散列导致的哈希冲突。

s123

初始容量

初始数字长度，根据 initialCapacity 计算的得到，计算的方法是 tableSizeFor：
cap 就是 initialCapacity.

static final int tableSizeFor(int cap) {  
    int n = cap - 1;  
    n |= n >>> 1;  
    n |= n >>> 2;  
    n |= n >>> 4;  
    n |= n >>> 8;  
    n |= n >>> 16;  
    return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;  
}

目的是取大于等于 initialCapacity 的 2 的 n 次幂的数，比如 initialCapacity 为 8 则返回 8，initialCapacity 如果是 15，则返回 16。

n |= n >>> 1 先将 n 友移 1 位，再与原来的 n 求活运算，实际的结果是把 n 最高位右边的第一位设置为 1。n |= n >>> 2 以及后面一直到 16 都一样，将 n 最高位的 1 右边的所有位都设置为 1。此时再针对 n 操作 + 1，刚好整体进 1 位，得到一个 2 的 n 次幂的数。

针对 cap 的减一操作是为了针对 cap 已经是 2 的 n 次幂的数场景，如果不减 1，假设 cap 为 8，那么最终的结果会是 16。只有对 cap 减 1 以后，最终得出的结果才是 8。
https://www.cnblogs.com/loading4/p/6239441.html

如果默认构造器，也就是不指定任何参数，那么 hash 表数组初始化的长度是 DEFAULT_INITIAL_CAPACITY，也就是 16。
默认的初始数组长度如果太小，容易造成过多的 rehash，太大又容易浪费内存空间，16 是一个经验值。

加载因子

如果初始容量大于最大条目数除以负载因子，则不会发生重新哈希操作。

1	threshold = capacity * load factor

HashMap 中的键值对数量超过阈值 threshold 时会扩容数组，threshold 会有一个初始值，初始值通过 tableSizeFor 计算得到，前面已经描述过。
在每次扩容以后，下一次的扩容阈值 threshold 为 capacity 乘以加载因子，capacity 为扩容后的数组长度。

put 方法

public V put(K key, V value) {
    // 对key的hashCode()做hash
    return putVal(hash(key), key, value, false, true);
}

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
    Node<K, V>[] tab;
    Node<K, V> p;
    int n, i;
    // 步骤①：tab为空则创建
    if ((tab = table) == null || (n = tab.length) == 0)
        n = (tab = resize()).length;
    // 步骤②：计算index，并对null做处理 
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);
    else {
        Node<K, V> e;
        K k;
        // 步骤③：节点key存在，直接覆盖value
        if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k))))
            e = p;
        // 步骤④：判断该链为红黑树
        else if (p instanceof TreeNode)
            e = ((TreeNode<K, V>) p).putTreeVal(this, tab, hash, key, value);
        // 步骤⑤：该链为链表
        else {
            for (int binCount = 0; ; ++binCount) {
                if ((e = p.next) == null) {
                    p.next = newNode(hash, key, value, null);
                    // 链表长度大于8转换为红黑树进行处理
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st  
                        treeifyBin(tab, hash);
                    break;
                }
                // key已经存在直接覆盖value
                if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e;
            }
        }

        if (e != null) { // existing mapping for key
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e);
            return oldValue;
        }
    }

    ++modCount;
    // 步骤⑥：超过最大容量 就扩容
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict);
    return null;
}

冲突处理：不同的 hash 值落到 hash 表相同的桶时，采用链表处理。

1.8 版本，链表长度达到一定程度以后，链表转为红黑树。在 put 的时候，如果 hash 冲突，并且尾插法入链以后链表长度超过 8，此时尝试将链表转化为红黑树。

操作链表转红黑树的方法 treeifyBin：

final void treeifyBin(Node<K,V>[] tab, int hash) {  
    int n, index; Node<K,V> e;  
	// 在hash表数组长度小于64时，先执行rehash，尝试通过rehash拆分链表
    if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)  
        resize();  
	// 链表转红黑树
    else if ((e = tab[index = (n - 1) & hash]) != null) {  
        TreeNode<K,V> hd = null, tl = null;  
        do {  
            TreeNode<K,V> p = replacementTreeNode(e, null);  
            if (tl == null)  
                hd = p;  
            else {  
                p.prev = tl;  
                tl.next = p;  
            }  
            tl = p;  
        } while ((e = e.next) != null);  
        if ((tab[index] = hd) != null)  
            hd.treeify(tab);  
    }  
}

哈希表扩容

JDK 1.7

void resize(int newCapacity) {  
    Entry<?,?>[] oldTable = table;  
    int oldCapacity = oldTable.length;  
    if (oldCapacity == MAXIMUM_CAPACITY) {  
        threshold = Integer.MAX_VALUE;  
        return;  
    }
    Entry<?,?>[] newTable = new Entry<?,?>[newCapacity];  
    transfer(newTable, initHashSeedAsNeeded(newCapacity));  
    table = newTable;  
    threshold = (int)Math.min(newCapacity * loadFactor, MAXIMUM_CAPACITY + 1);  
}

void transfer(Entry<?,?>[] newTable, boolean rehash) {  
    Entry<?,?>[] src = table;  
    int newCapacity = newTable.length;  
    for (int j = 0; j < src.length; j++) {  
        Entry<K,V> e = (Entry<K,V>)src[j];
        // 沿着链表将所有的节点迁移到新数组
        while(null != e) {  
            Entry<K,V> next = e.next;
            if (rehash) {  
                e.hash = null == e.key ? 0 : hash(e.key);  
            }
            int i = indexFor(e.hash, newCapacity);
            // 在链表的头部插入
            e.next = (Entry<K,V>)newTable[i];
            // 维护数组的索引执行Entry
            newTable[i] = e;
            e = next;
        }  
    }  
}

遍历老哈希表数组，如果数组位存在链表结构，则用 k-v 节点的 next 引用遍历整个链表。
针对遍历到的每个 k-v 节点，根据 hash 值计算在新数组上的下标，再在对应位置的链表头部插入当前 k-v 节点。

JDK 1.8

final Node<K, V>[] resize() {
    Node<K, V>[] oldTab = table;
    int oldCap = (oldTab == null) ? 0 : oldTab.length;
    int oldThr = threshold;
    int newCap, newThr = 0;
    if (oldCap > 0) {
        // 超过最大值就不再扩充了，就只好随你碰撞去吧
        if (oldCap >= MAXIMUM_CAPACITY) {
            threshold = Integer.MAX_VALUE;
            return oldTab;
        }
        // 没超过最大值，就扩充为原来的2倍
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                oldCap >= DEFAULT_INITIAL_CAPACITY)
            newThr = oldThr << 1; // double threshold
    } else if (oldThr > 0) // initial capacity was placed in threshold
        newCap = oldThr;
    else {               // zero initial threshold signifies using defaults
        // 首次初始化
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int) (DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
    // 计算新的resize上限
    if (newThr == 0) {
        float ft = (float) newCap * loadFactor;
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float) MAXIMUM_CAPACITY ?
                (int) ft : Integer.MAX_VALUE);
    }
    threshold = newThr;
    @SuppressWarnings({"rawtypes"，"unchecked"})
    Node<K, V>[] newTab = (Node<K, V>[]) new Node[newCap];
    table = newTab;
    if (oldTab != null) {
        // 把每个bucket都移动到新的buckets中
        for (int j = 0; j < oldCap; ++j) {
            Node<K, V> e;
            if ((e = oldTab[j]) != null) {
                oldTab[j] = null;
                if (e.next == null)
                    newTab[e.hash & (newCap - 1)] = e;
                else if (e instanceof TreeNode)
                    ((TreeNode<K, V>) e).split(this, newTab, j, oldCap);
                else { // 链表优化重hash的代码块
                    Node<K, V> loHead = null, loTail = null;
                    Node<K, V> hiHead = null, hiTail = null;
                    Node<K, V> next;
                    do {
                        next = e.next;
                        // 原索引
                        if ((e.hash & oldCap) == 0) {
                            if (loTail == null)
                                loHead = e;
                            else
                                loTail.next = e;
                            loTail = e;
                        }
                        // 原索引+oldCap
                        else {
                            if (hiTail == null)
                                hiHead = e;
                            else
                                hiTail.next = e;
                            hiTail = e;
                        }
                    } while ((e = next) != null);
                    // 原索引放到bucket里
                    if (loTail != null) {
                        loTail.next = null;
                        newTab[j] = loHead;
                    }
                    // 原索引+oldCap放到bucket里
                    if (hiTail != null) {
                        hiTail.next = null;
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    return newTab;
}

不同场景的扩容（resize）

1、调用无参数构造器初始化

1	HashMap map = new HashMap();

newCap 取 DEFAULT_INITIAL_CAPACITY，也就是 16。
newThr 取 DEFAULT_INITIAL_CAPACITY 乘以 DEFAULT_LOAD_FACTOR，也就是 16 乘以 0.75，也就是12。

2、调用有参数构造器初始化

1	HashMap map = new HashMap(4, 0.75f);

newCap 取初始化时算出的 threshold，也就是 4，threshold 的初始化逻辑见前述的「初始容量」小节。
newThr 取 newCap 乘以 loadFactor（加载因子），loadFactor 的值为构造函数传入的值。

3、容量超过 threshold 以后的扩容
newCap 取当前数组容量 oldCap 的两倍
newThr ：

1、如果当前数组容量 oldCap 大于等于 16（DEFAULT_INITIAL_CAPACITY），newThr 取当前的 threshold（oldThr）乘以 2。
2、如果小于，newThr 取 newCap 乘以 loadFactor（加载因子），loadFactor 的值为构造函数传入的值。

关于第一点有个疑问：这种场景，为什么要取 oldThr 乘以 2 ？

答：首先有个规则，当数组容量 capacity 大于 MAXIMUM_CAPACITY 时， threshold 取 Integer.MAX，也就是不再扩容，无视 hash 碰撞。在 capacity 小于 MAXIMUM_CAPACITY 时，threshold 的计算方法永远是 capacity 乘以 loadFactor。
那么当 capacity 未达到 MAXIMUM_CAPACITY 时，capacity 每次扩容都是乘以 2，loadFactor 不变，threshold 的计算如下：

1	threshold = newCap * loadFactor = (oldCap * 2) * loadFactor = (oldCap * loadFactor) * 2

又因为

1	oldCap * loadFactor = oldThreshold

所以

1	threshold = oldThreshold * 2

计算逻辑经过转化以后，可以直接用位运算体现乘法，能提升性能：

1	newThr = oldThr << 1; // double threshold

这里的逻辑，如果 oldCap 乘以 2 以后超过了 MAXIMUM_CAPACITY，那么 threshold 也要取最大值，也就是 Integer.Max。这部分逻辑在后面提现：

// 计算新的resize上限
if (newThr == 0) {
    float ft = (float) newCap * loadFactor;
    // 当newCap超过MAXIMUM_CAPACITY，newThr取Integer.MAX_VALUE
    newThr = (newCap < MAXIMUM_CAPACITY && ft < (float) MAXIMUM_CAPACITY ?
            (int) ft : Integer.MAX_VALUE);
}

1.8 针对扩容的变化

首先 k-v 节点从老哈希表迁移到新哈希表时，新的数组下标的计算采用了新的方式。
1.7 采用取模方式：

static int indexFor(int h, int length) {  
    // assert Integer.bitCount(length) == 1 : "length must be a non-zero power of 2";  
    return h & (length-1);  
}
// 外层的调用逻辑
int i = indexFor(e.hash, newCapacity);
... = newTable[i];

1.8 的方式，简化后的代码

// oldCap为扩容前的哈希表数组长度
// j为在扩容前的哈希表数组的下标
if ((e.hash & oldCap) == 0) {
	newTab[j] = ..;
}
else {
	newTab[j + oldCap] = ..;
}

这里用 hash 值和扩容前的哈希表数组长度求余，得到 0 时，在新数组的下标不变；在非 0 时，在新数组的下标为老数组下标加 oldCap。

为什么能这么处理呢？本质上这里也是为了做取余。

前面「hash函数」小节中已经提到过，h & (n-1) 其实是对 n 取模。如果 n 的位数减一是 A，那么这个取模运算本质是取二进制 h 的右边 A 位。更详细的见前面的小节。

扩容以后，新数组的容量扩展为原来的 2 倍，也就是 n 的二进制位数多一位，取余的计算则是对二进制 h 取右边 A + 1 位。
那么这个时候就要看多出的一位是 1 还是 0 了。

如果是 0，则取余结果，也就是新数组的下标和原数组下标一致，
如果是 1，则取余结果，也就是新数组的下标为原数组下标 + 原数组容量。

自己的分析：光就取模运算本身，也就是计算在新数组的下标这个点上，其实没什么差别，在性能上没有明显的区别。那么为什么用做这个变动呢？

1.8 的方式就计算新下标本身是和 1.7 没什么区别，有意思的点是 1.8 的方式明确知道了 hash 值在新数组的下标要么是 j，要么是 j + oldCap。猜测可以利用这个点做一些优化。

网上一般的说法，可以在并发下，避免 1.7 transfer 方法链表成环，造成死循环。
1.7 头插法造成死循环的原因： https://tech.meituan.com/2016/06/24/java-hashmap.html 「线程安全性」一节

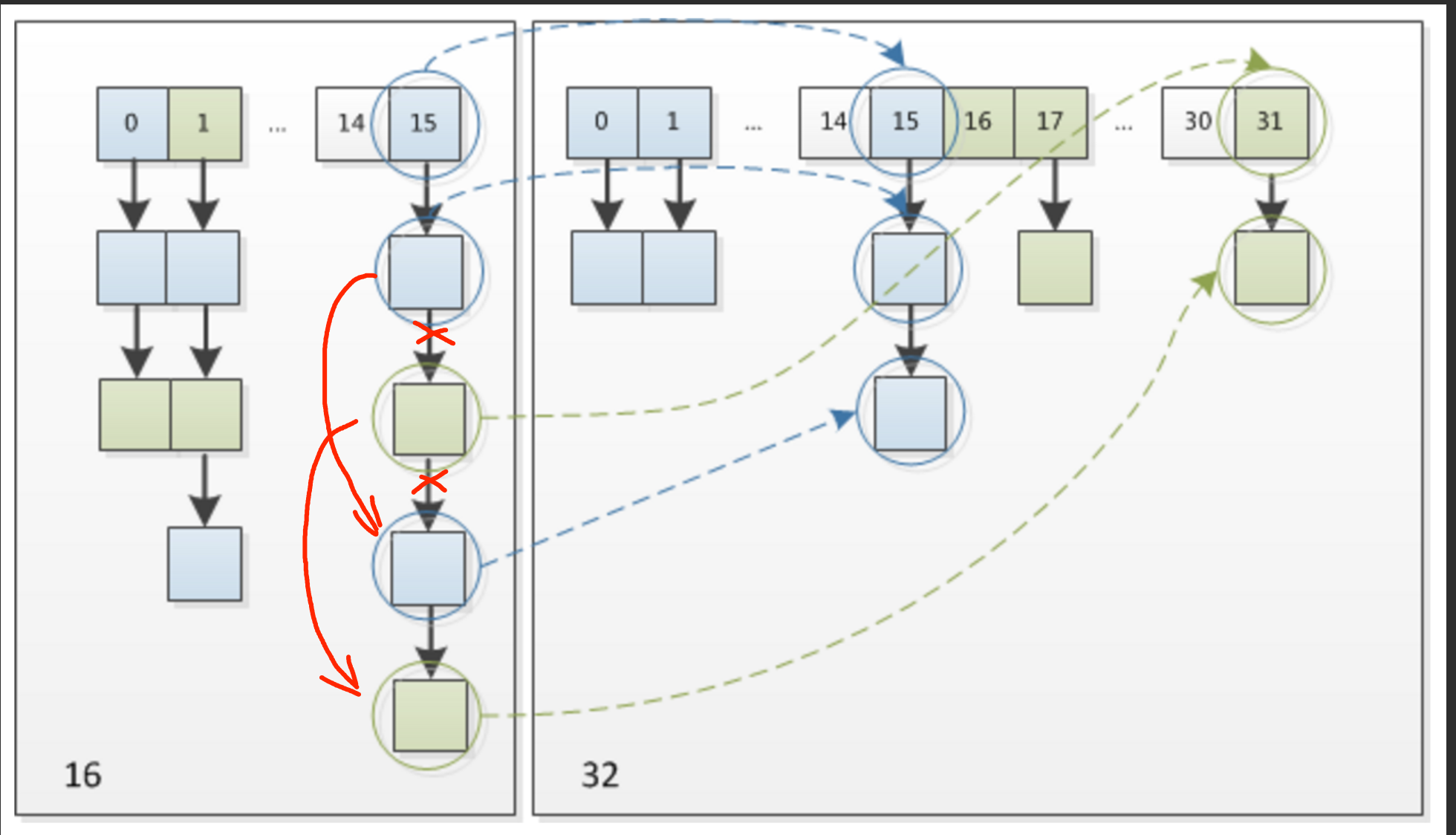
1.8 能避免的原因：1.8 的的 transfer 过程采用尾插法，如图，在针对原数组 15 这个位置的链表进行 rehash 时，如果有其他线程同时执行 rehash。。。。。TODO

[

假设一个线程执行完以后 transfer 以后，下图左侧就是原链表的结构。如果此时被中断的线程开始从头执行 transfer 过程，那么会丢掉部分数据，而不会造成循环。

PS 此处总觉研究起来没啥意义，因为 HashMap 本来就不应该用在并发场景下，再研究在一个错误使用场景下的细节的点没什么特别的意义。

扩容针对红黑树的处理

for (int j = 0; j < oldCap; ++j) {
    Node<K,V> e;
    if ((e = oldTab[j]) != null) {
        oldTab[j] = null;
        if (e.next == null)
            // 原hash桶不存在冲突
            newTab[e.hash & (newCap - 1)] = e;
        else if (e instanceof TreeNode)
            // 原hash桶已经转为红黑树
            ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
        else { // preserve order
            // 原hash桶为链表
            // ....
        }
    }
}

当原 hash 表的节点为红黑树节点时，执行红黑树的拆分，拆分成两部分，一部分在原位置，也就是 j，一部分在 j + oldCap。

final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
    TreeNode<K,V> b = this;
    // Relink into lo and hi lists, preserving order
    TreeNode<K,V> loHead = null, loTail = null;
    TreeNode<K,V> hiHead = null, hiTail = null;
    int lc = 0, hc = 0;
    for (TreeNode<K,V> e = b, next; e != null; e = next) {
        next = (TreeNode<K,V>)e.next;
        e.next = null;
        // 新数组的下标为原数组下标一致
        if ((e.hash & bit) == 0) {
            if ((e.prev = loTail) == null)
                loHead = e;
            else
                loTail.next = e;
            loTail = e;
            ++lc;
        }
        // 新数组的下标为原数组下标 + 原数组容量
        else {
            if ((e.prev = hiTail) == null)
                hiHead = e;
            else
                hiTail.next = e;
            hiTail = e;
            ++hc;
        }
    }
	// 落到低位，也就是原数组下标
    if (loHead != null) {
	    // 当红黑树的容量 <= 6 时，将红黑树退化为链表
        if (lc <= UNTREEIFY_THRESHOLD)
            tab[index] = loHead.untreeify(map);
        else {
            tab[index] = loHead;
            if (hiHead != null) // (else is already treeified)
                loHead.treeify(tab);
        }
    }
    // 落到低位，也就是原数组下标 + 原数组容量
    if (hiHead != null) {
	    // 当红黑树的容量 <= 6 时，将红黑树退化为链表
        if (hc <= UNTREEIFY_THRESHOLD)
            tab[index + bit] = hiHead.untreeify(map);
        else {
            tab[index + bit] = hiHead;
            if (loHead != null)
                hiHead.treeify(tab);
        }
    }
}

那么为什么链表元素超过 8 个转为红黑树，少于 6 个转为链表？

红黑树的平均查找长度是log(n)，长度为8，查找长度为log(8)=3，链表的平均查找长度为n/2，当长度为8时，平均查找长度为8/2=4，这才有转换成树的必要；链表长度如果是小于等于6，6/2=3，虽然速度也很快的，但是转化为树结构和生成树的时间并不会太短。

还有选择6和8的原因是：

中间有个差值7可以防止链表和树之间频繁的转换。假设一下，如果设计成链表个数超过8则链表转换成树结构，链表个数小于8则树结构转换成链表，如果一个HashMap不停的插入、删除元素，链表个数在8左右徘徊，就会频繁的发生树转链表、链表转树，效率会很低。
https://www.cnblogs.com/aaabbbcccddd/p/14849064.html

引申一 HashMap 的各种遍历方式

1、entrySet + foreach 方式

for (Map.Entry<String, String> entry : map.entrySet()) {  
    entry.getKey();  
    entry.getValue();  
}

entrySet 返回了一个 HashMap 内部实现的 Set，他的元素类型是 Entry<K, V>，EntrySet 实现 Iterable，通过实现一个 Iterator 完成遍历。

final class EntryIterator extends HashIterator  
    implements Iterator<Map.Entry<K,V>> {  
    public final Map.Entry<K,V> next() { return nextNode(); }  
}
abstract class HashIterator {  
    Node<K,V> next;        // next entry to return  
    Node<K,V> current;     // current entry  
    int expectedModCount;  // for fast-fail  
    int index;             // current slot  
    HashIterator() {  
        expectedModCount = modCount;  
        Node<K,V>[] t = table;  
        current = next = null;  
        index = 0;  
        if (t != null && size > 0) { // advance to first entry  
            do {} while (index < t.length && (next = t[index++]) == null);  
        }  
    }
    public final boolean hasNext() {  
        return next != null;
    }
    final Node<K,V> nextNode() {  
        Node<K,V>[] t;
        Node<K,V> e = next;  
        if (modCount != expectedModCount)  
            throw new ConcurrentModificationException();  
        if (e == null)  
            throw new NoSuchElementException();  
		// 在链表上查找下一个节点
        if ((next = (current = e).next) == null && (t = table) != null) {  
            // 在一个hash桶已经遍历完时，在hash数组上遍历寻找下一个非null的桶
            do {} while (index < t.length && (next = t[index++]) == null);  
        }  
        return e;  
    }
}

另外 keySet 本质上也一样，也是通过 HashIterator 作为迭代器。

final class KeyIterator extends HashIterator  
    implements Iterator<K> {  
    public final K next() { return nextNode().key; }  
}

引申：网上大部分的的 HashMap 遍历测试都支出，lambda 的方式性能较差：

1
2
3

map.forEach((k, v) -> {  
    //  
});

比如：https://mp.weixin.qq.com/s/zQBN3UvJDhRTKP6SzcZFKw
原因是 lambda 首次执行耗时会长，后续就没那么长了，原因见 https://juejin.cn/post/6844904202439753741
简单说就是在初次执行时需要加载额外的框架，用于加载 lambda 本身，但是这个开销是一次性的，因此在真实开发的时候可以不用纠结这个地方的性能。相反，普遍认为 lambda 的方式可读性更好。

资料

https://tech.meituan.com/2016/06/24/java-hashmap.html
https://zhengw-tech.com/2019/06/01/java-rehash/

HashMap原理分析

http://footmanff.com/2024/03/03/2024-03-03-Java-HashMap-1/

Author

张阿力

Posted on

2024-03-03

Updated on

2024-04-22

Licensed under

#HashMap

HashMap原理分析

hash函数

初始容量

加载因子

put 方法

哈希表扩容

JDK 1.7

JDK 1.8

不同场景的扩容（resize）

1.8 针对扩容的变化

扩容针对红黑树的处理

引申一 HashMap 的各种遍历方式

资料

Author

Posted on

Updated on

Licensed under

Catalogue